-
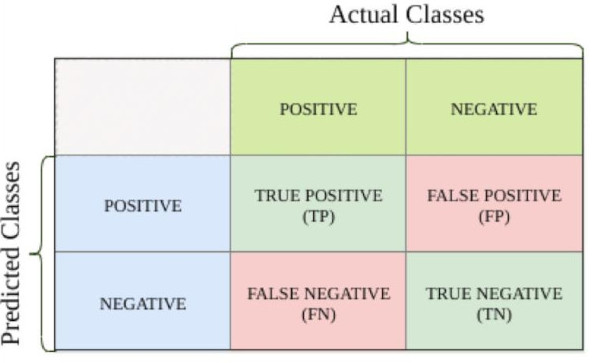
Precision: The proportion of true positive predictions out of all positive predictions made by the model.
\[Precision = \frac{True Positives}{True Positives + False Positives}\]-
Precision is critical in scenarios where “false positives” are costly, such as spam detection or medical diagnoses (predicting a disease that doesn’t exist).
-
-
-
Recall (Sensitivity or True Positive Rate) (Độ nhạy): The proportion of true positive predictions out of all actual positive cases in the dataset.
\[Recall = \frac{True Positives}{True Positives + False Negatives}\]- Recall is crucial in situations where false negatives are costly, such as detecting fraud or identifying critical system errors.
-
Accuracy: The proportion of all correct predictions (both positives and negatives) out of the total predictions.
\[Accuracy = \frac{True Positives + True Negatives}{Total Predictions}\]-
Useful when the dataset has balanced classes but can be misleading in imbalanced datasets.
-
-
-
F1 Score: The harmonic mean of precision and recall, balancing the two metrics.
\[F1-score = 2 \times \frac{Precision \times Recall}{Precision + Recall}\]- Ideal for imbalanced datasets where you want to balance false positives and false negatives
-
Log Loss (Logarithmic Loss): A metric for evaluating the probability predictions of a classification model. It quantifies how close the predicted probabilities are to the true labels.
\[LogLoss = \frac{1}{N} \sum^{N}_{i=1} [y_{i}log(p_{i}) + (1-y_{i})log(1-y_{i})]\]- Where:
- $y_{i}$ is a label [0,1]
- $p_{i}$ is predicted probability for the positive class.
- Important in probabilistic models like logistic regression, where accurate probability calibration is key.
- Where:
-
ROC AUC (Receiver Operating Characteristic - Area Under Curve): For classification problems in ML, you want to minimize the False Positive Rate (predict that the user will return and purchase and they don’t) and maximize the True Positive Rate (predict that the user will return and purchase and they do).
- Value Range:
- 0.5: Random guess.
- 1.0: Perfect model.
-
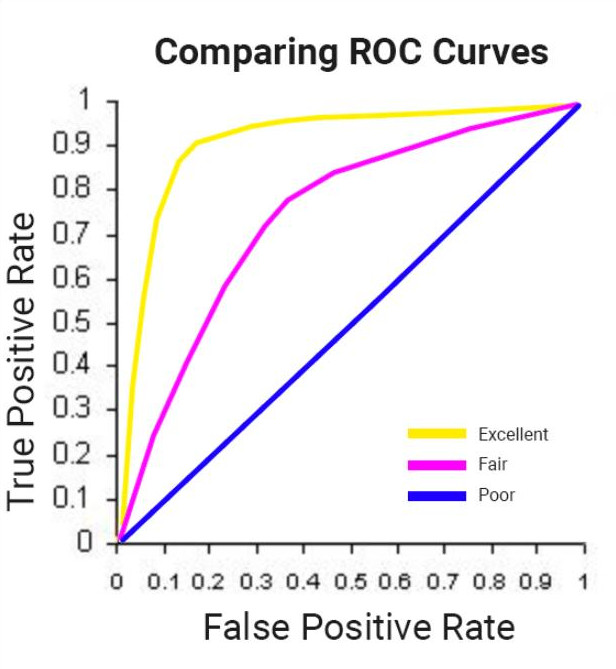
- Useful for binary classification, especially in imbalanced datasets, as it evaluates model performance across all classification thresholds.
- Value Range:
