In artificial intelligence (AI), “activations” and “normalization” are heard regularly but it’s not easy to differentiate them because both are just a type of mathematical transformation.
A. ACTIVATIONS: refers to the process of mapping the “linear outputs” of neurons to a “non-linear range”, so the network can learn “complex patterns”. Sometimes activation is also to keep a “good gradient flow” to avoid “varnishing gradient” problem.
There are 4 types of Activation Functions: Sigmoid, Tanh, ReLU, Softmax.
-
Sigmoid: output between 0, 1, often used in classification
\[\sigma(x) = \frac{1}{1 + e^{-x}}\]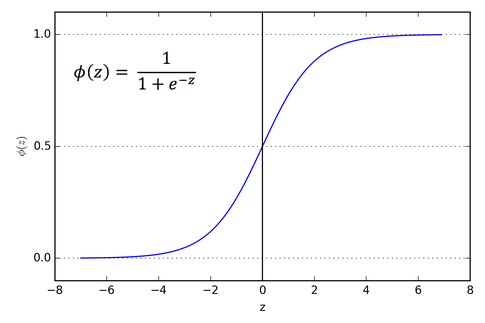
Figure 1: Sigmoid
-
Tanh: output between -1 to 1, centered around 0. It is better for input datas that are complicated with both negative and positive information like “words data”.
\[\tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}\]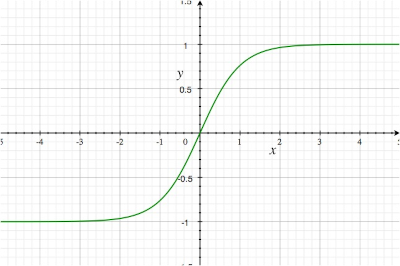
Figure 2: Tanh
-
ReLU (Rectified Linear Unit): Introduces sparsity (sự thưa thớt) and avoids vanishing gradients.
\[f(x) = max(0, x)\]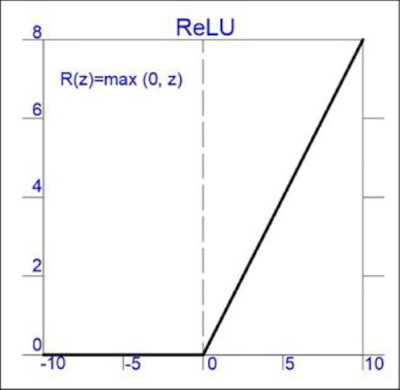
Figure 3: ReLU
- Explaination of “vanishing gradient” : Based on the learning equation:
Because the gradients of $Sigmoid$ and $Tanh$:
\[d_{sigmoid} = \sigma(x) \cdot (1 - \sigma(x))\] \[d_{tanh} = 1 - tanh^{2}(x)\]- Both $d_{sigmoid}$ and $d_{tanh}$ are very small (~0) when x (or W) is far greater than 0, so that the back propagarion(sự lan truyền) through the layers of neurons will become slower. In contrast, ReLU gradient is always 1 with x > 0, this will accelerate the backward propagation or the learning. However, $ReLU$ still has a probelm that gradient is always zero when x $\le$ 0. This is called “dying ReLU problem”.
-
Softmax: Converts logits to probabilities for multi-class classification, given a vector $\vec{z}$ = [$z_{1}$, $z_{2}$,… , $z_{n}$]:
\[softmax(z_{i}) = \frac{e^{z_{i}}}{\sum_{j=1}^{n} {e^{z_{j}}}} = s_{i}\]after applying softmax, we have $\vec{z}$ = [$s_{1}$, $s_{2}$,… , $s_{n}$] with:
\[\sum_{i=1}^{n} {s_{i}} = 1\]
B. NORMALIZATION: a technique to transform a set of values to have a specific scale or statistical property. “Normalization” means to stabilize training by avoiding large fluctuations via activations across layers, making values to be between 0 and 1 again before each layer, while keeping its relative distribution and helping improve “convergence” (sự hội tụ).
-
Data Normalization (before training):
\[x' = \frac{x - \mu}{\sigma}\]With:
- $\mu$: mean of the input data.
- $\sigma$: “standard deviation” of the data, squared root of “variance” $\sigma^{2}$
-
Batch Normalization (during training): used to “normalizes” activations within a mini-batch.
\[y_{i} = \gamma \cdot x'_{i} + \beta, \ \ x'_{i} = \frac{x_{i} - \mu_{B}}{\sqrt {\sigma^{2}_{B} + \epsilon}}\]With:
- $\epsilon$ : prevent the denominator from being zero.
- $\mu_{B}, \ \sigma^{2}_{B}$: mean and variance of the batch.
- $\gamma, \ \beta$: learnable parameters for scaling and shifting respectively.
